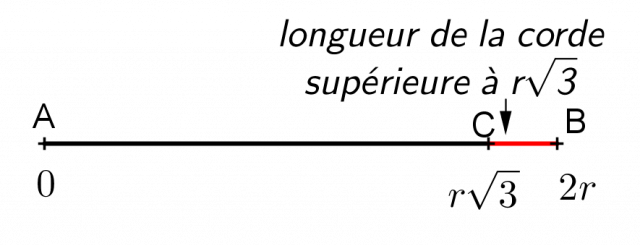La genèse de la notion de probabilité
Pascal répond d’abord à cette question : la mise de chaque joueur étant de 32 pistoles chacun, et sachant que le premier qui gagne trois parties, remporte les 64 pistoles, comment partager les 64 pistoles si on interrompt la partie lorsqu’un joueur a gagné exactement deux fois et l’autre une seule fois ?
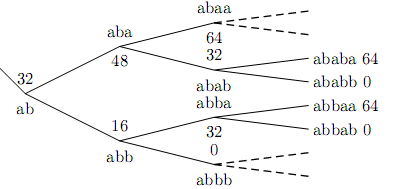
Pascal fait l’hypothèse de l’équiprobabilité de chaque lancer de dés et reconstitue les 8 parties possibles si le jeu ne s’était pas interrompu : abaa, abab -ababa, abab-ababb, etc... et estime à chaque fois la somme à verser au joueur a. Si le jeu est gagnant 64, jeu égal 32, jeu perdu 0 et enfin moyenne des gains pour obtenir 48 et 16 pistoles.
|
XVIIIe et XIXe siècles – L’étude de cette nouvelle branche des mathématiques.
En particulier, ils mettent en évidence le lien entre statistique (étude de caractère à l’aide d’un échantillon) et probabilité. Par exemple, si on lance 10 000 fois un dé et que l’on comptabilise le nombre de « six » obtenus, la fréquence d’apparition du six dans cet échantillon est un calcul de statistique. La loi des grands nombres dit alors que cette fréquence est "proche" de la probabilité 1/6, plus précisément la fréquence est comprise dans un intervalle de longueur environ 0.02 centré sur 1/6.
Cette notion est à l’origine des sondages. On remarquera que seule la taille de cet échantillon est importante. Faire un sondage dans l’Orne, en France ou en Chine ne requiert pas plus de sondés (au moins 1 000).
1933 – La modélisation théorique
Les probabilités sont « jeunes » (300 ans pour les calculs, 80 ans pour la théorie) au regard des autres notions mathématiques comme la géométrie euclidienne (5 000 ans) ou même l’analyse.
1890 - Le paradoxe de Bertrand
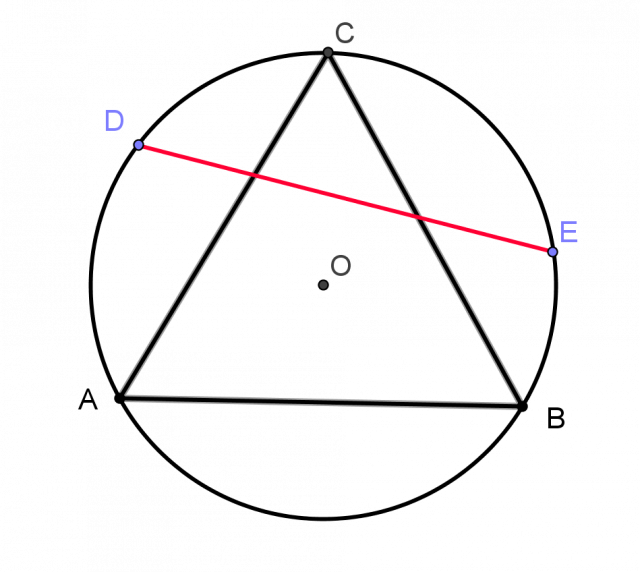
: Traçons au hasard une corde dans un cercle, quelle est la probabilité qu’elle soit plus longue que le côté du triangle équilatéral inscrit dans ce cercle.
La question qu’il faut se poser est : que signifie « tracer au hasard une corde » ?
Quatre possibilités qui engendrent quatre probabilités.
Possibilité 1 : les cordes sont parallèles à une direction donnée.
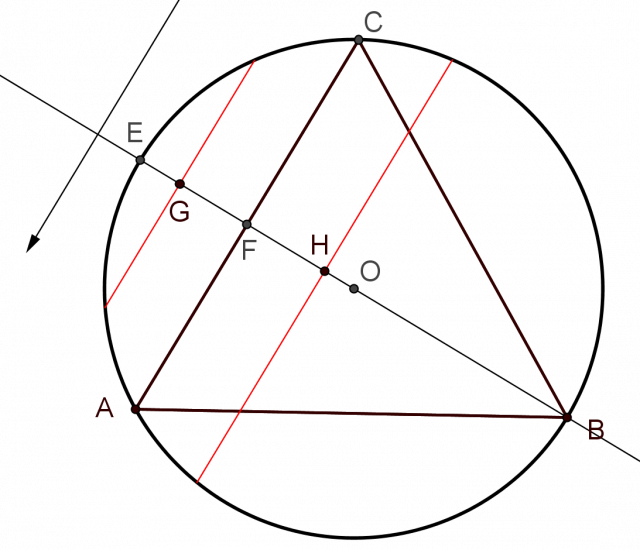
Le choix de cette direction puis de la corde sont équiprobables puis du fait des propriétés de symétrie du triangle équilatéral, il suffit de se restreindre à la position du point d’intersection entre la corde (en rouge sur la figure) et le rayon perpendiculaire OE.
Si ce point (G ou H sur la figure) appartient au segment [OF], alors la corde est plus grande que le côté du triangle. Il est alors évident (les distances EF et OF sont égales, voir figure) que la probabilité cherchée vaut 1/2.
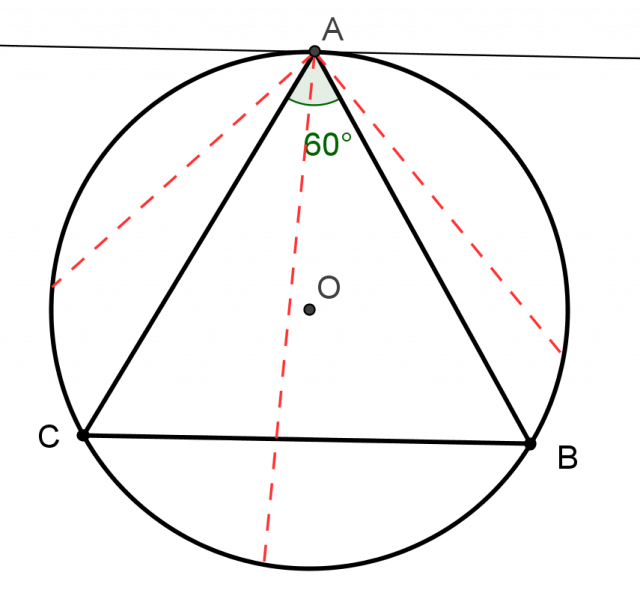
Possibilité 2 : fixer un point sur le cercle et faire "tourner" l’autre extrémité sur le cercle.
Si l’autre point se situe sur l’arc BC alors la corde est plus grande que le côté du triangle. Cela correspond à 60° et comme la corde balaye un angle de 180°, la probabilité cherchée est donc 1/3.
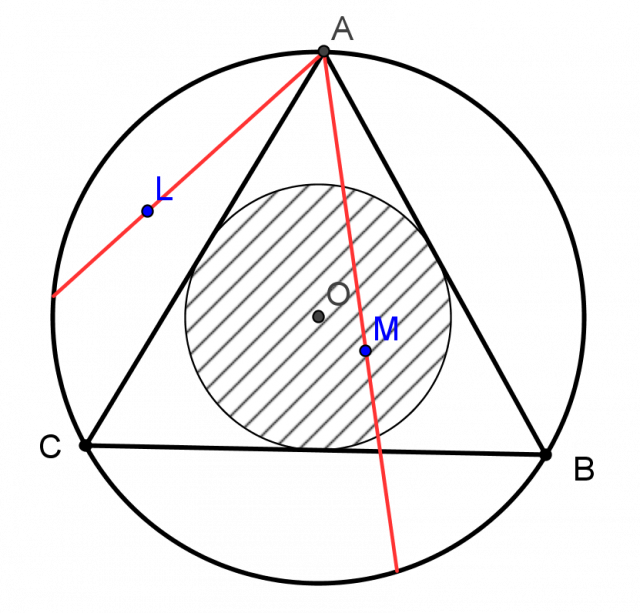
Possibilité 3 : choisir un point au hasard à l’intérieur du cercle et tracer une corde passant par ce point.
Toujours par des considérations de symétrie liées au cercle et au triangle équilatéral, la corde est plus grande que le côté du triangle lorsque le point choisi appartient au cercle inscrit dans le triangle (hachuré sur le dessin).
On sait que ce cercle a un rayon deux fois plus petit que celui du grand cercle et donc une aire 4 fois plus petite. La probabilité cherchée vaut 1/4.
Possibilité 4 : une fois la corde tracée, calculer sa longueur et la comparer à la longueur du côté d’un triangle équilatéral.
Un calcul simple, faisant appel à la trigonométrie du collège, permet de constater que la longueur du côté du triangle vaut r √3. La longueur de la corde doit donc être comprise entre cette valeur et le diamètre soit 2r (voir figure ci-dessus). La probabilité cherchée est égale, selon la répartition uniforme des réels, au rapport de la longueur BC par la longueur AB soit BC/AB = (2 - √3)/2 environ 0.134.
Voir en ligne : Le paradoxe de Bertrand.