Prophétie
Nikolaï Lobatchevski (1792-1856) est l’inventeur de la « géométrie hyperbolique » dont le postulat est : « par un point pris hors d’une droite passe plusieurs parallèles ». Ce postulat a comme conséquence, entre autre, que la somme des angles d’un triangle mesure moins de 180° et que les triangles semblables n’existent pas.
L’avenir ne cesse de lui donner raison, car l’univers technologique dans lequel nous baignons doit énormément, en pratique, à des travaux abstraits de mathématiciens du passé qui œuvraient sans souci d’utilité, juste pour la beauté et la cohérence de leurs théories. Ainsi les courbes de Peano, conçues il y a un siècle comme de purs jeux esthétiques, permettent de dessiner des antennes radio.
COURBE DE PEANO (Courbe étudiée par Peano en 1890)
Définition : La courbe de Peano est une courbe remplissant le carré de côté 1 définie par l’algorithme suivant :
| Première étape | Deuxième étape | Et la suite ... | |
|---|---|---|---|
Partager le carré en 9 « petits » carrés « égaux » ; numéroter chacun de ces carrés de sorte que deux carrés successifs se touchent par un côté, en commençant par le carré en bas à gauche, et terminant par le carré en haut à gauche ; il y a deux possibilités : nous choisissons le chemin vertical. 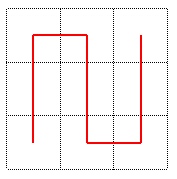
étape 1
|
Partager chacun de ces carrés en 9 « micro » carrés « égaux » ; numéroter chacun de ces carrés de sorte que deux micro carrés successifs se touchent par un côté, en commençant par le micro-carré en bas à gauche et terminant par le micro-carré en haut à droite, le premier micro-carré d’un petit carré devant avoir un côté en commun avec le dernier micro-carré du petit carré précédent et le dernier micro-carré devant toucher par un coté le petit carré suivant. 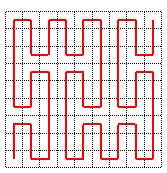
étape 2
|
Recommencer ce processus à l’infini. 
courbe de Péano
|
COURBE DE HILBERT 3D
| Première étape | Deuxième étape | Et la suite ... |
|---|---|---|
Partager le cube de côté 1 en 8 « petits » cubes « égaux » ; numéroter chacun de ces cubes de 1 à 8 de sorte que deux cubes successifs se touchent par une face. 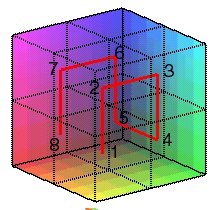
étape 1
|
Partager chacun de ces carrés en 8 « micro » cubes « égaux » ; numéroter chacun de ces cubes de sorte que deux micro cubes successifs se touchent par une face, le premier micro-cube d’un petit cube devant avoir un côté en commun avec le dernier micro-cube du petit cube précédent et le dernier micro-cube devant toucher par une face le petit cube suivant.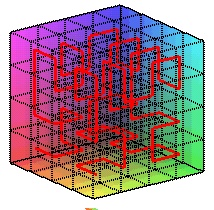
étape 2
|
Recommencer ce processus à l’infini. 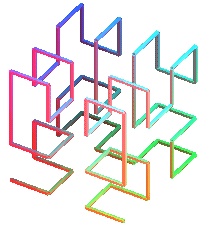
courbe de Hilbert
|
Cette courbe a une longueur très grande dans volume restreint. Les industriels de la téléphonie portable l’utilise pour leur antenne. Vous téléphonez avec une courbe de Hilbert !
Conclusion
Les prodigieux développements de l’arithmétique, de l’analyse statistique, de la logique – conduits au nom de la recherche fondamentale – se retrouvent dans les codages qui ont permis les cédéroms et les DVD, la compression des données informatiques, le téléphone portable, le wi-fi, les télé-paiements sécurisés, etc. Les abstractions mathématiques sont entrées au service de l’imagerie médicale, de l’architecture des micro-processeurs, de la prévision météo, des modèles climatiques, de l’analyse boursière ou de l’évaluation du risque d’extinction de telle ou telle espèce vivante....
C’est ainsi que le monde moderne, pour devenir toujours davantage performant, technologique et rationnel, a paradoxalement besoin de ces gourous des équations, de ces purs esprits qui fuient souvent le monde réel.
Extrait d’un article de Fabien Gruhier dans le numéro 2182 du Nouvel Observateur







